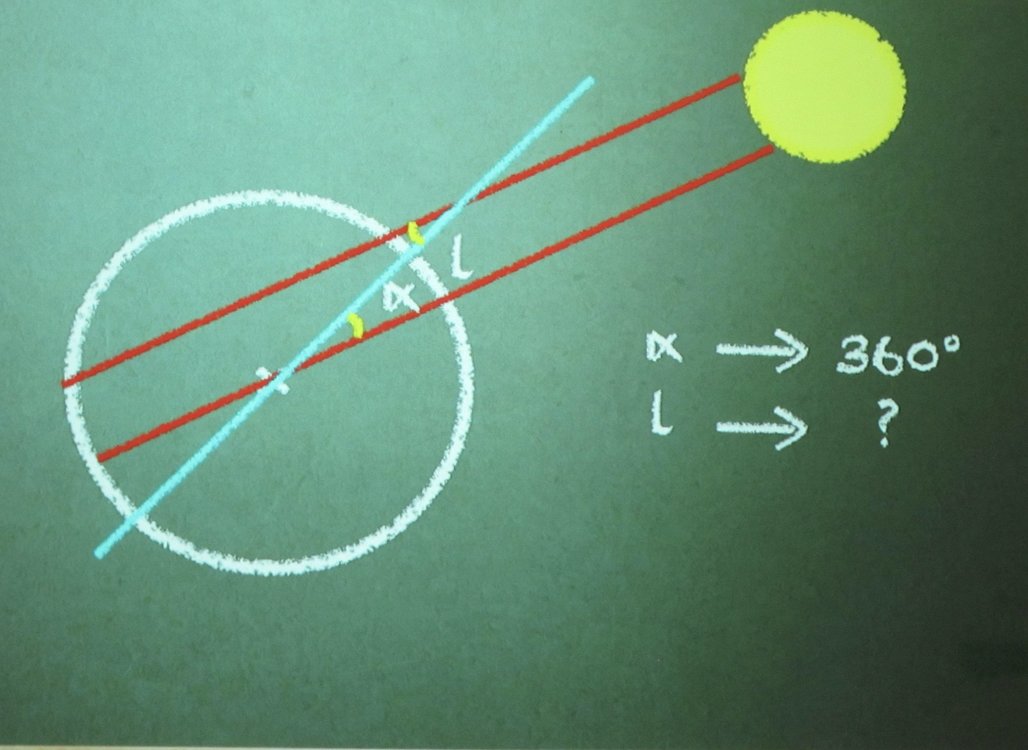
Pour faire la démonstration Ératosthène a eu besoin de la propriété suivante. Si deux droites parallèles sont coupées par une droite sécante alors les angles alternes-internes qu’elles forment sont de la même mesure.

A Alexandrie, il a aussi utilisé un bâton, gnomon, pour mesurer un angle, soit l’ombre portée du bâton. L’angle de 7,2 ° est trouvé à l’aide de trigonométrie. 

Il a également eu besoin d’un calcul de proportionnalité que l’on peut réaliser à l’aide d’un tableau de proportionnalité.

Pour passer de 7,2° à 360° il faut faire x 50.

1 stade= 157,50 m donc 5000 stades =787500 m.

787500 x 50 = 39375000 m donc 39375km.

5000 x 50 = 250000 stades.

La circonférence réelle de la terre est de 40070 km et lui a trouvé 39 375km.

Le résultat de la circonférence de la Terre que Ératosthène a trouvé n’est pas tout à fait exact car on a découvert plus tard que la Terre n’est pas vraiment ronde, mais légèrement aplatie au niveau des pôles.

Co-auteurs : Bastien Guénon, Camille Petriat, Manon Seraphon, élèves de 5^e au collège Chambéry à Villenave d’Ornon en Gironde, avec l’aide de leur professeure Virginie Blanc et la documentaliste Patricia Vigier.

Réalisation des photos : Anaïs Faure et Janick Merlot, élèves de 5e.

La réalisation de cet article s’inscrit dans le dispositif « Sciences en collège », mené par Cap Sciences en partenariat avec le Conseil départemental de Gironde. Il vise, avec l’aide de la journaliste Marianne Peyri, à accompagner les collégiens dans l'écriture d’articles et la réalisation de photos ou vidéos rendant compte de projets artistiques, culturels ou scientifiques initiés par les collèges de Gironde.